When governments privatize their electricity sectors by selling off their electric generators, industry regulators must be mindful of potential anti-competitive behavior by the generators that may have negative effects on electricity customers.

Throughout the world, governments are realizing that their core competencies do not include the management and operation of electric utilities. Moreover, regulators now recognize that the traditional view of the electric utility as a natural monopoly is naive. Rather, regulators increasingly see an electric utility as three separate businesses: generation, transmission and distribution. The generation business is the one that consists of the actual power plants that produce electricity from coal, gas, hydro, nuclear or any of a number of sources. The transmission business transports power over high-voltage power grids, often over great distances, from the generators to electricity retailers. The distribution business uses lower voltage lines that distribute the power to domestic and most commercial and industrial customers. Distribution also includes metering, billing and other "last mile" services.

The Deregulated Electricity Market

After the separation of the generation, transmission and distribution functions there remains the need for coordination of demand and supply of electiricity. Demand is taken as given and supply is brought in as required. Deregulated electric generators offer generating capacity at a specified price. The coordinator of supply and demand ranks the supply offers from lowest to highest price per unit of electiricity to produce a supply curve -- the aggregate amount offered to the market by suppliers at each price.

To simplify matters, let's assume that each supplier of electricity (generator) offers all of its capacity at the same price. Further, that the plants are already "spinning" and so there are no startup costs. These assumptions simplify the analysis without materially affecting the results.

The system load (demand) is the amount of electricity needed to power all the electrical devices that are switched "on" at a given moment. Generators are dispatched (brought online) to meet the demand at the lowest cost. The cheapest plant is first dispatched, then the next cheapest plant, and so on, until all the load is met. A market clearing price (MCP) is then equated to the offer price of the last generator to come online. All the dispatched generators receive the MCP. Thus, although the first generator might have offered electricity at well below the MCP, it receives the MCP for each unit of power generated.

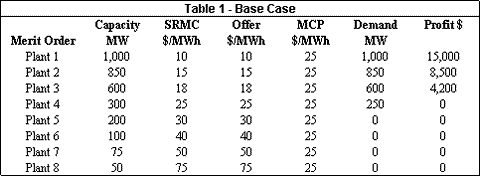
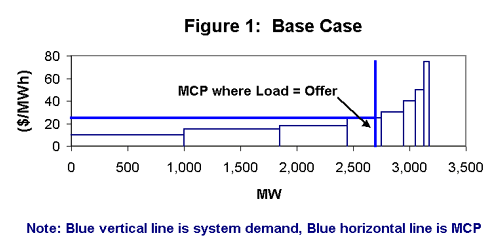
Table 1 lists the capacities and short run marginal costs (SRMC) of 8 sample electric generating plants. It also shows the price at which each generator is offering to supply power. Figure 1 shows how a system dispatcher would rank the offers to create a supply curve (which in this case is a step function). The system load is taken to be 2,700 megawatts (MW). Table 1 and Figure 1 show for comparison purposes a base case where each generator is offering electricity at its short-run marginal cost. Table 1 also shows the amount generated and the profit gained by each generator.

Bertrand Competition

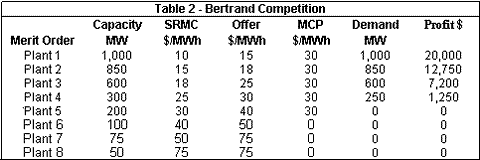
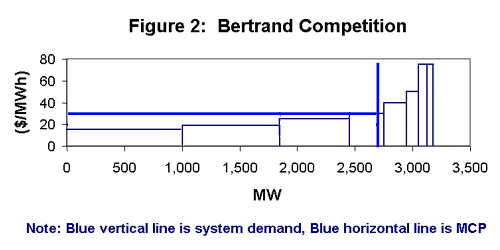
Typically, under a regime of perfect competition with no market power or gaming we observe a Bertrand offering strategy. In this case, each plant offers not its marginal cost, but rather the marginal cost of the next plant in the merit order. For example, Plant 1 offers the SRMC of Plant 2, etc. This is an optimal strategy because since plants never offer below their SRMC, each plant effectively has a monopoly in the price range below the SRMC of the next unit. Table 2 shows the offers and the profits under Bertrand competition. We note that the MCP has increased by $5 and all of the generators have increased their profits. Figure 2 shows the effect on the supply curve. Bertrand competition is the expected regime in a privatization. Its effects are worst when there are not many plants in the system and their marginal costs are drastically different. Regulators can mitigate the problem by minimizing the costs for new entrants who could exploit the discontinuities in the supply curve.

Merger of Adjacent Plants in the Merit Order

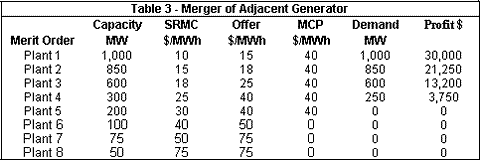
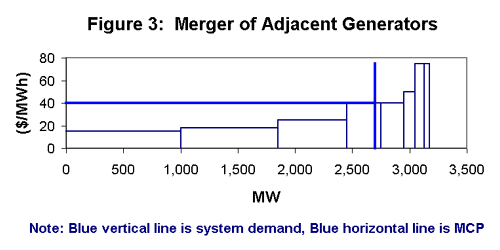
After the privatization occurs, regulators must institute safeguards against the merger of plants that are adjacent to each other in the merit order. In Table 3 we see the effects of the owner of Plant 4 purchasing Plant 5. In doing so, the owner can now offer Plant 4’s capacity up to Plant 6's SRMC (since he will face no competition from Plant 5). Although Plant 5 is not run, the MCP has been pushed up to $40 and profits have increased. Figure 3 shows the supply curve under such an arrangement. The implication for the regulators is that when privatizing the generators two things must occur: 1) Plants that are adjacent to each other should not be owned by the same operator, 2) Post-privatization mergers must be scrutinized to prevent the merger of adjacent plants.

The Exercising of Market Power by a Large Generator

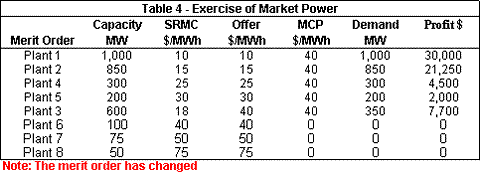
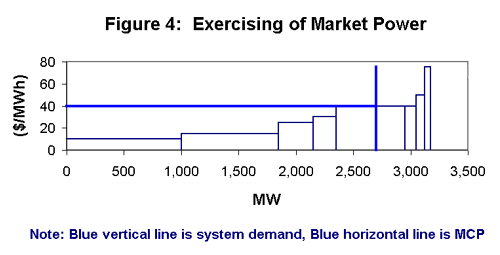
During the privatization process, regulators must ensure that large plants are not able to exercise market power to raise prices. This can be done through many creative measures including special fuel contracts, etc. In Table 4 we see the effect of Plant 3 "gaming" the system by offering at the marginal cost of Plant 6 (not shown, assumed to be $40). This is called offering "out of merit" since the merit order no longer corresponds to the SRMC of the plants. Since Plant 3 is large, it is able to offer a high price resulting in a new merit order. In this scenario, unlike the previous three, Plant 5 is dispatched. Interestingly, Plant 3 is not dispatched to its full capacity, yet its ability to raise the MCP increases its profits over the Bertrand case. This is demonstrated in Figure 4.

 The Exercising of Market Power by a Large Generator

As we have seen in four examples, the market price of electricity can be dramatically affected by the regime in which generators operate. Table 5 summarizes the market prices and profits earned by the generating companies under each scenario. From this table, it becomes clear that regulators must carefully consider issues of gaming and market power when privatizing their electric generators.