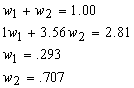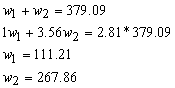|
Capital
Markets
Homework
Answers –
Session 4 Topic: Bond Price Volatility and Managing Interest
Rate Risk
a)
First, consider an upward shift of 100 basis points (+1.00% to
9.032%). What is the new
price of the bond? b)
Given
the shift in a), what was the percentage price change of the bond? c)
Now,
consider a downward shift of 100 basis points (-1.00% to 7.032%)
instead. What is the new
price of the bond? d)
Given
the shift in c), what was the percentage price change of the bond? (Your
answers are a first look at price volatility. Duration (a measure of
price volatility) is a very important concept we will cover next week in
the course.) Answer:
Increase the yield to 9.032% and the price becomes 84.236 for a
loss of 10.38%. If the
yield decreases to 7.032% the price is 105.818 for a gain of + 12.573%.
What we learn from this problem is that the price change is not
linear in the yield change. That is, the price-yield relationship is a curved
(non-linear) one. 2.
Calculate the Macaulay duration and the Modified duration of the
Treasury strip maturing on August 15, 2006 as of Jan 15, 1998.
Assume the yield is 6.39%. Remember
that the Mac Duration of a zero-coupon bond is simply the bond’s
maturity. As such, this
bond’s Mac Duration is simply its maturity of 8.58 years (as of Jan.
15, 1998). The Modified duration is just D(Mac)/1.032
(use semi-annual rates). In
numerical terms, we get: 8.58
/ 1.032 = 8.31 3. Calculate the durations (Macaulay and Modified) of the 8% Treasury note maturing on January 15, 2002 as of January 15, 1997. Assume the yield is 6.0%., For this problem you can use equal-length semi-annual periods, although you may have learned by now that it is not exactly correct in the Treasury market (where actual days to each payment date are used). What problems might you anticipate if you had calculated the durations as of Jan. 10th or Jan. 20th? The duration of the Treasury note is calculated by
spreadsheet as follows:
Mac Duration = 923.42 / 108.50
= 8.51 half years.
In full years, the Mac Duration can thus be expressed as 4.25
years. Therefore, Mod Duration is 4.25/(1+.03)=4.13 4.
Suppose
the liabilities of an insurance company consist of an annual
end-of-the-year cash outflow (for pension obligations) of $100 for each
of the next 5 years. To
fund these obligations over the next five years, the insurance company
can make investments in two bonds that pay annual (end-of-the-year)
coupon interest. These bonds include a one-year bond with a 6 percent coupon
and a four-year bond with an 8 percent coupon.
Both bonds have a face value of $100.
The interest rate (yield) is currently 10 percent for all
maturities. a)
Calculate
the present value of the liability. b)
Calculate
the duration of the liability. c)
Calculate
the duration of each of the bonds (assets). d)
The
company desires to immunize its liability against interest rate
fluctuations. To do this,
the firm needs to set the Macaulay duration of its liabilities
equal to the Macaulay duration of its assets.
Given the durations of the assets (bonds) and the liability
above, how much of each bond does the firm need to buy to immunize the
liability? e)
Later
in the same day that you purchased the two bonds, the interest rate
falls to 9.5%. Recalculate
the value of the assets and the liability after this drop.
Is the liability immunized? Why or why not? Suppose the interest rate had risen to 10.5% (from the
original 10%). Recalculate
the value of the assets and liability after this rise.
Is the liability immunized? Why or why not? f)
Why would the insurance
company want to immunize its liability?
What risk would the insurance company have incurred if it had not
immunized the liability? To immunize its liabilities, the insurance company
needs to set the Mac Duration of its assets equal to the Mac Duration of
its liabilities. With
immunization, the value of its liabilities will remain equal to the
value of its assets when interest rates move.
Remember that these bonds pay annual
coupons and compound interest annually
as well. (We choose to use
annual compounding for ease of calculation.
Technically, for US bonds, we would “officially” use
semi-annual compounding.) a)
Liabilities
- calculating the present value
therefore, PV=$379.07 b)
Duration
=
(Remember that the duration of a zero-coupon bond
equals its maturity! If you
were to do the math below, you would arrive at the same answer.)
PV=96.36 therefore
Duration =
Four Year Bond with 8% Coupon
PV=93.66Duration =
d)
To
meet its pension obligations over the next five years, the company needs
to purchase an investment portfolio whose present value and duration
equals that of its
liabilities. In other
words, it needs to invest $379.07 into the two bonds and allocate this
investment across the two bonds such that the bond portfolio has a
duration of 2.81. Computation of portfolio proportion, w1 and w2.
The company should put 29.3% of its investment in
Bond 1 and 70.7% in Bond 2 in order to achieve a duration of 2.81 for
the portfolio. Number of Bonds held (at 10% discount rate)
Another way to think of this problem is in
duration-weighted dollars. Then
your two equations in two unknowns are:
which gives you the answer in terms of dollars
instead of proportions. e)
Present
Values:
Present
Values of Asset Portfolio and Liability Stream:
Note: The
asset portfolio value is computed as the number of units held of each
bond (see answer in (d)) times the present values. f)
If
the company were to not
immunize its liabilities, the value of its asset portfolio could fall
below the value of its liability obligations if interest rates were to
shift. In other words, the
company would run the risk of not being able to meet its pension obligations and becoming
insolvent.
|